１　学年及び単元名

第1学年　　たしざん（２）

２　単元のねらい

加法の意味を理解し、それらを用いることができるようにする。（※単元の評価規準表）

３　単元の設定について

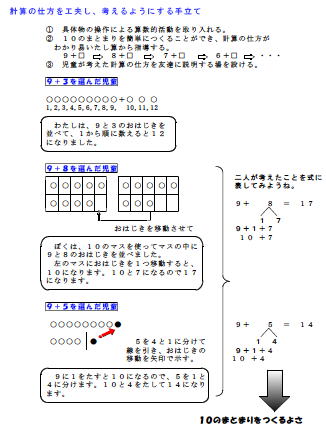
　本単元では、「たしざん(１)」、「20までのかず」及び「３つのかずのけいさん」に基づいて、(１位数)＋(１位数)の和が(十何)になる場合の計算方法の理解と習熟を図ることをねらいとしている。具体的操作から念頭操作に移っていきながら、10の補数を見つけて加数を分解する計算方法のよさを知り、進んで生活に生かそうとする態度を養うことのできる単元である。今後、「ひきざん（２）」、「100までのかず」へと発展し、２年生以降の四則計算の基礎となる単元と言える。
　１０時間という長時間の単元であるため、本学級の子どもたちが入学以来親しんでいるぬいぐるみ「かずくん」とのかかわりをストーリーにした単元構成をし、学習することに必要感をもたせるようにした。１年生にとって、架空のお話（ごっこ遊び）はとても魅力的なものである。自分が主人公になることにより、課題意識をもって楽しく主体的に学習に取り組むと考えた。
　指導にあたっては、児童の実態を考慮し、具体的操作や図で表す活動を十分取り入れて、計算の方法を工夫し考えることができるようにしたい。また、課題を選択できるようにし、お互いの解決方法を聞き合う場を設定することにより、多様な考えを知る機会とし、中でも10の補数を見つけて加数を分解する考えのよさを十分感じ取らせたい。繰り上がりのあるたし算36通りは、随時、たし算カードを使って習熟させるとともに、学習のまとめにおいて、カードを使ったゲームで興味や意欲を引きだし、楽しく計算練習ができるように配慮したい。さらに、式から問題をつくる活動を取り入れ、加法の意味の理解が深まるようにしたい。

３　単元の目標

○　加法が用いられる場面について知り、式で表したり、式を読んだりすることができるようにする。
○ (１位数)＋(１位数)の繰り上がりのある計算に興味をもち、その計算の方法について考えることができるようにする。
○　(１位数)＋(1位数)の繰り上がりのある計算の仕方を理解し、確実に計算することができるようにする。

４　指導計画　（総時数　１０時間）

第１次　繰り上がりのあるたし算の算法（７時間）
　・被加数が９のたし算の算法の理解　　
　・被加数が８のたし算の算法の理解　　
　・被加数が７のたし算の算法の理解　　
　・被加数が６のたし算の算法の理解（本時４／７）
　・被加数が６以上のたし算の練習（カード）
　・被加数が５以下のたし算の算法の理解　
　・被加数が５以下のたし算の練習（カード）　
第２次　繰り上がりのあるたし算のまとめ（３時間）
　・たしざんカードによる計算練習
　・たし算の適用題と問題づくり　　　　

５　指導事例

単元全体の課題　　「かずくん」にたしざんのやり方を教えてあげよう

かずくん	かずくんの手紙の概略　いたずら者の弟ぷうたは、森の神様を怒らせてつかまってしまいました。プウタを返してほしかったら、ぼくの苦手な計算ができるようになれと言われて困っています。ぼくは、答えが10より大きくなるたしざんがよくわからないんだ。１年生のみんな、ぼくにたしざんのやり方を教えてくれませんか。お願いします。

課題意識を持たせ、意欲を継続させる手立て

１　ストーリー性のある学習課題
　総時数10時間の「たしざん(２）」は、１年生にとって、課題意識を持続させるには難しい単元である。クマのぬいぐるみ「かずくん」はクラスの友達として、これまで一緒に学習したり、遊んだりしてきた。
　そこで、「かずくん」を主役にしたストーリーを学習課題にして、学習意欲を喚起し、「かずくん」との手紙のやりとりを通して意欲を継続させることにした。

児童の反応（発言）
　「かずくんには弟がおったんやね。」
　「かずくん、計算が苦手なん。」
　「教えてあげるよ。」

　「かずくんは、答えが10より大きくなるたしざんがわからないって、書いているよ。」と「かずくん」の手紙の内容に目を向けさせ、学習課題を意識させる。

２　式の選択、具体物の選択
　９＋２から９＋９を板書して、８つの式の中から自分が計算方法を考えたい式を選択させた。計算方法を考えるために使いたい具体物も自分で選んでよいことにした。（８＋□、７＋□、・・・・も同様）

児童の反応
　「ブロックとマスのある操作盤を使おう。マスがあると数えやすいよ。」
　「磁石つきのおはじきと操作盤を使おう。たされる数とたす数のおはじきの色を変えるとよくわかるよ。」
　「たされる数もたす数も○を書いて考えよう。操作盤のマスに書くと数えやすいな。操作盤を使おう。」

計算の仕方を工夫し、考えるようにする手立て

　　　　　手だて

＊　８＋□、７＋□の計算の仕方を考えるときには、１０のまとまりをより効率的につくろうする児童が増えてきた。
＊７＋□や６＋□の学習のときは、被加数よりも加数の方が大きくなる場合が増えるため、被加数を分解して１０のまとまりをつくる方法も出てくる。そのような児童の考えのよさに気づかせるためにも、いろいろなやり方を比較・検討する場を大切にしたい。


	話し合いを深めるための手立て
		１　話し合いの手順や方法を示す。２　子どもたちの話し合いで不十分な点を補足したり、話し合いの視点を与えたりしながら、話し合いを深める。 ③　考え方のよさや記述のよさ、その子ならではの工夫を見取り、評価する。

子どもたちの考えのよさ

６＋８
　被加数をハートで、加数を星で表現している。加数の８から４をとり、６に加えて10のまとまりを作っている。４つの星がどこに移動したのか、わかるように線を引いている。

４＋８
　被加数４を分解して10のまとまりを作る。移動した数２やできた10のまとまりを表示している。色ちがいのおはじきを使って、被加数と加数を区別している。

６＋６
　10マスを２列ほど使っている。１列目の１個目から６個目のマスに斜めの線をひき、「６」と表示した。次にたす数の６個分を７個目のマスから同様に斜め線を引いていった。２列目の２個分まで斜め線が引けたので、答えは12と判断している。数え足しのようだが、10と２という見方もできている。

２＋９
　数図ブロックと操作盤の10マスを使っている。加数を分解するより、被加数の２から加数の９へ１つ移動する方が簡単だと気づいている。

話し合いの後、かずくんに手紙を書かせ、その時間の評価の一助とした。

手紙の記述

かずくんへ
　９＋７のこつを教えるね。９こおはじきをおきます。したに７こおいて、７こから１ことって９このほうにおくと、こたえがでるよ。10こと６こになるから、こたえがみえたね。かずくん、ぷうたがみつかるといいね。けいさんがんばってね。

たしざんの習熟のために（たしざん名人になろう）

　　　　　　　たし算習熟のために

子どもの作った問題

　教科書にはない「星」という素材を使って、問題をつくっています。

　教科書の問題を参考にして、つくりました。

　ハムスターを飼っている児童の問題です。