小学校算数：　数と計算の意味について理解する　５年

１　学年及び単元名

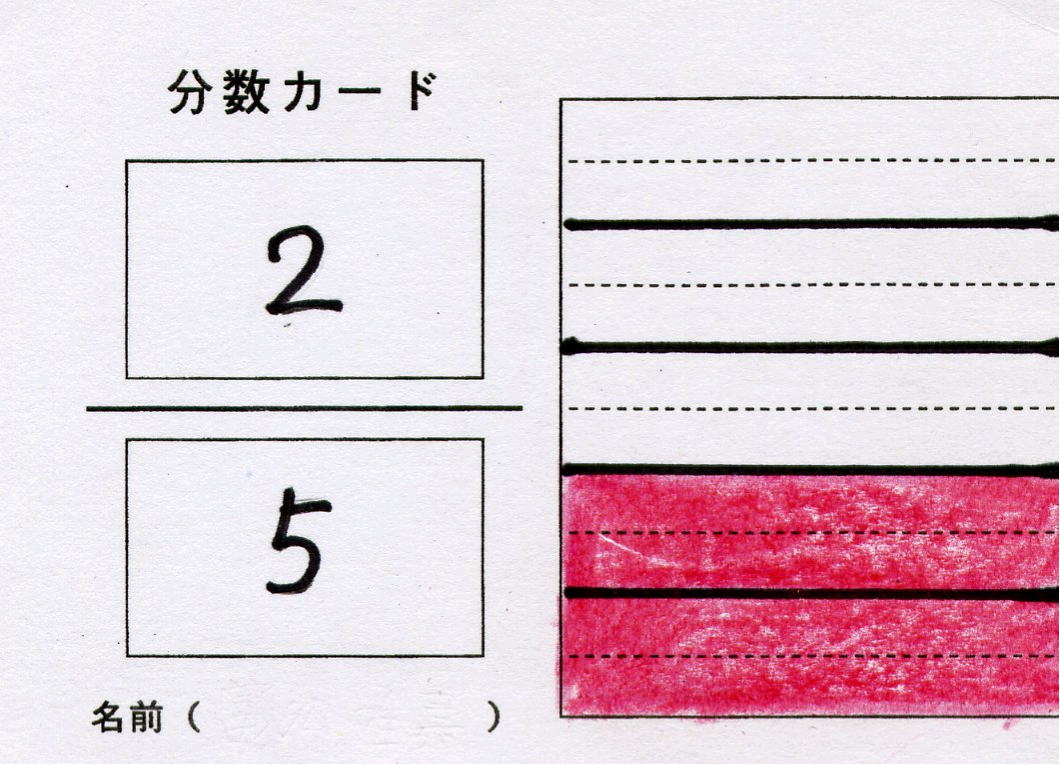
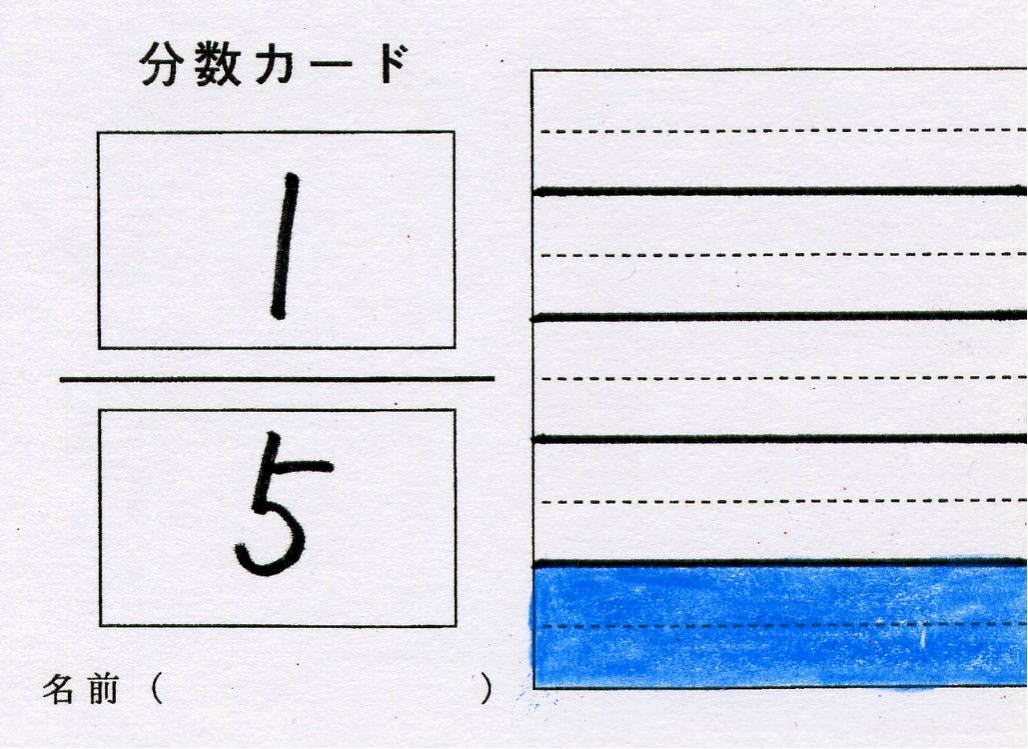
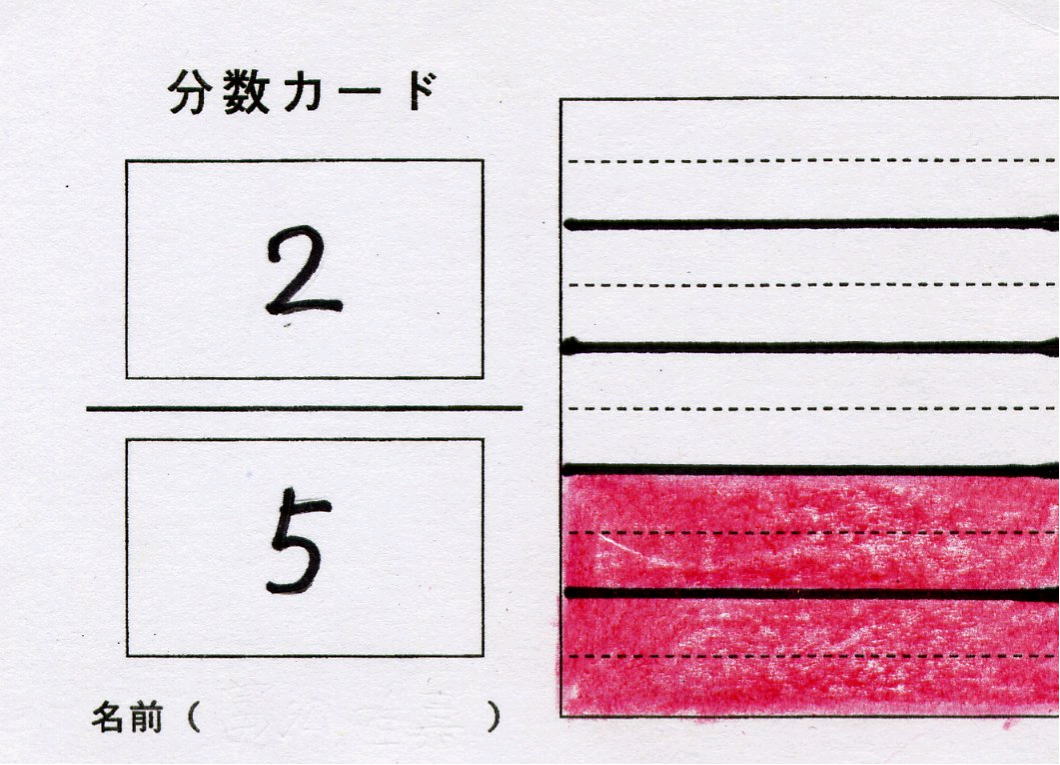
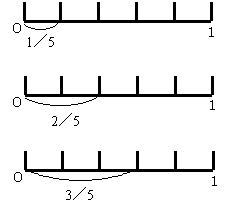
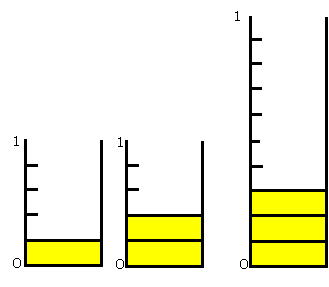
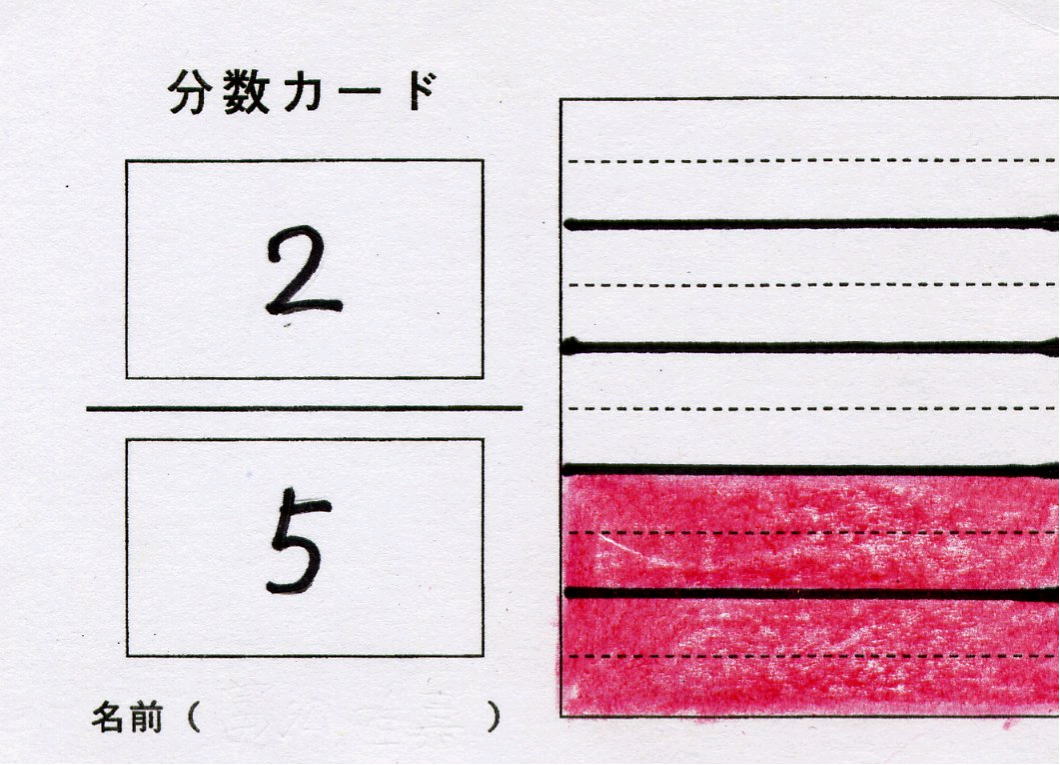
第５学年　　分数～分数カードを使って～

２　単元のねらい

　分数についての理解を深めるとともに、同分母の分数の加法および減法の意味について理解し、それらを適切に用いることができるようにする。（※単元の評価規準表）

３　単元を組み立てる視点

　４年で、端数部分の表し方を考えるところから分数が導入され、用語やそれらの意味、単位分のいくつ分という見方、数直線上の点との対応、いろいろな分数の種類（真分数・仮分数・帯分数）があることを学習してきている。しかしながら、分数の意味の理解が不十分な児童や量のイメージができ上がっていない児童もいる。分数を理解する上で、数の大きさをイメージしにくいことが一つの障壁として存在すると考えられる。
　そこで、以下の点に留意し、単元を組み立てた。

４　指導計画（１２時間）

第一次　分数の大きさ・・・・・・・・・・・・・２時間★（※本時案　１／２）
第二次　分数のたし算とひき算・・・・・・５時間
第三次　わり算と分数・・・・・・・・・・・・・２時間
第四次　分数と小数，整数・・・・・・・・・３時間

５　実践事例

　分数カードで量感をイメージする

１～１０までの数で分数カードをつくろう

＜条件＞

　・同じ数を２回使わないこと。

　・分子より分母の方が大きいこと。

　　　　　　　　　　　　　　　　　　　　　　　（※分数カード）

　　１～１０までの数を使って分数を作り、その大きさを面積図に表す。一人が５枚のカードを作る。

　 分数カードで大きさ比べをする

　分数カードで、隣の人と大きさ比べをする。活動の中で、分母が同じものや分子が同じものの
大きさに気付いたり、大きさの等しい分数があることに気付いたりする。

　・分母が同じ分数の大きさ　

　　　１　　２　　３　　４　　５

　　　－＜－＜－＜ー＜－

　　　５　　５　　５　　５　　５

　・分子が同じ分数の大きさ　

　　　１　　１　　１　　１　　１　　１　　１　　

　　　－＜－＜－＜ー＜－＜－＜－

　　　８　　７　　６　　５　　４　　３　　２　　

　・大きさの等しい分数

　　　１　　２　　３　　４　　５

　　　－＝－＝－＝ー＝－

　　　２　　４　　６　　８　　10

　同じ分母のものを集め、分数階段を作る。学級全体で行い、足りないカードは作っていく。分母が同じ分数、分子が同じ分数の大小を面積図で視覚的に確認しながら、分数の大小関係についてまとめていった。１～１０までの数字を使う場合、カードは全部で４５種類である。

　 分　数　階　段

分母が同じ分数を比べる

分子が同じ分数を比べる
１
－
２	分数カードの活用により理解できたこと
１　　２
－　－
３　　３
１　　２　　３
－　－　－
４　　４　　４
１　　２　　３　　４
－　－　－　　－
５　　５　　５　　５
１　　２　　３　　４　　５
－　－　－　　－　－
６　　６　　６　　６　　６
１　　２　　３　　４　　５　　６
－　－　－　　－　－　－
７　　７　　７　　７　　７　　７
１　　２　　３　　４　　５　　６　　７
－　－　－　　－　－　－　－
８　　８　　８　　８　　８　　８　　８
１　　２　　３　　４　　５　　６　　７　　８
－　－　－　　－　－　－　－　　－
９　　９　　９　　９　　９　　９　　９　　９
１　　２　　３　　４　　５　　６　　７　　８　　９
－　－　－　　－　－　－　－　　－　－
10　 10 　　10　　10　　10　 10 　 10　　10　 10

　　分数カードを使って計算の仕方を考える

	ジュースが２つのびんに、1／5リットルと2／5リットルはいっています。あわせて何リットルですか。

　本単元では、計算の仕方を図などで表現する作業的・探求的な算数的活動を取り入れた。問題把握の場面では、実際の色水や分数カードを示し、視覚的に計算の仕方を考えるように促す。児童は、「あわせて」という言葉を手がかりに、分数のたし算であることに気付き、自力解決の場面では、「私は面積図で考えよう」、「ぼくはテープ図が分かりやすい」というように、それぞれの方法で計算の仕方を考えていた。