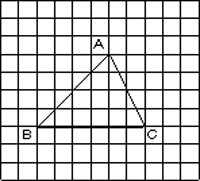
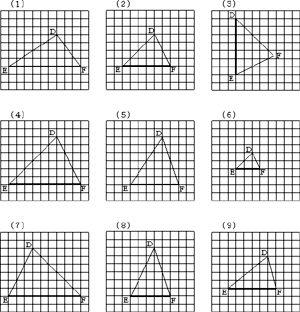
１ 単元名　　第３学年　「相似な図形」 ２ 単元評価規準　　hyou_01.pdf へのリンク（別紙） ３ 単元設定の意図 　「大きいものを縮小したり、小さいものを拡大したりして、考えやすい大きさにする。」といった活動は、地図や設計図、写真や映画、望遠鏡や顕微鏡、模型など、生徒にとっても身近な存在である。この単元では、このように拡大や縮小を行うときに図形を構成する要素のうち、変化するものと変化しないものに着目して、特に対応する線分の変化の仕方やその関係を分析する。こうした活動により、図形の相似の概念を明らかにするとともに，三角形の相似条件をもとにして図形の性質についての理解をいっそう深めることになる。 　現行の学習指導要領より、それまで小学校の第６学年で学習していた「縮図や拡大図」は、「図形の合同」とともに、中学校での学習内容に統合されることになった。したがって、これまで「拡大したり縮小したりした図形」や「重なり合うことのできる図形」として、「相似な図形」や「合同な図形」の存在や特徴について小学校において多少の学習経験があったといえるが、現行の学習指導要領においては、従来小学校で取り扱ってきた操作活動を取り入れた学習を、中学校でも丁寧に扱いながら相似や合同に関する概念形成を図る必要がある。 　また、中学校での学習内容においても「相似な図形」が、第２学年から第３学年へと移行している。それにともなって、第３学年という発達段階を鑑みると、単元「相似な図形」で扱う論証の課題においては、それまでの数学科の授業や総合的な学習の時間での学習経験を生かして解決できるような、広がりや深まりを内包した課題を用意することも必要である。 　相似と合同に関する学習が、第２学年と第３学年の２学年に渡って行われることで、指導の一貫性が損なわれる可能性があるので、指導に当たっては、特に「面積が等しい図形」と「形が同じ図形」のインタラクションとして「合同な図形」が存在するといった概念の包含関係を意識した指導が必要である。 　この単元の指導において、思考力、判断力、表現力を確かなものにする工夫として、生徒に「選ぶ・並べる・分ける」といった活動を展開することにした。